N乗硬化塑性体のくびれ発生条件 1 真応力真ひずみ曲線 1 真応力真ひずみ曲線 まず、一般的な真応力真ひずみ曲線は①に示す。 材料を引っ張ると、まず真ひずみの小さい領域で 弾性変形 がおこる。 弾性変形はいわゆるバネと同じで、材料を引っ張る隣接する2つの原子面の面間隔dは、ミラー指数hklと格子定数の関数である。立方晶の対称性をもつ結晶では d=a/√(h^2 k^2 l^2) ・・・(1) となる。 質問:「(1)式を証明せよ」と言われたのですが、どうす その他(教育・科学・学問) 解決済 教えて!gooHkl d hkl = a h2 k2 l2 a:格子定数 面間隔 7
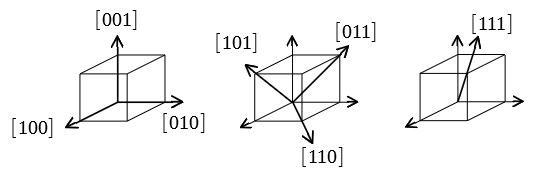
ミラー指数による立方晶 六方晶における面と方向の表し方
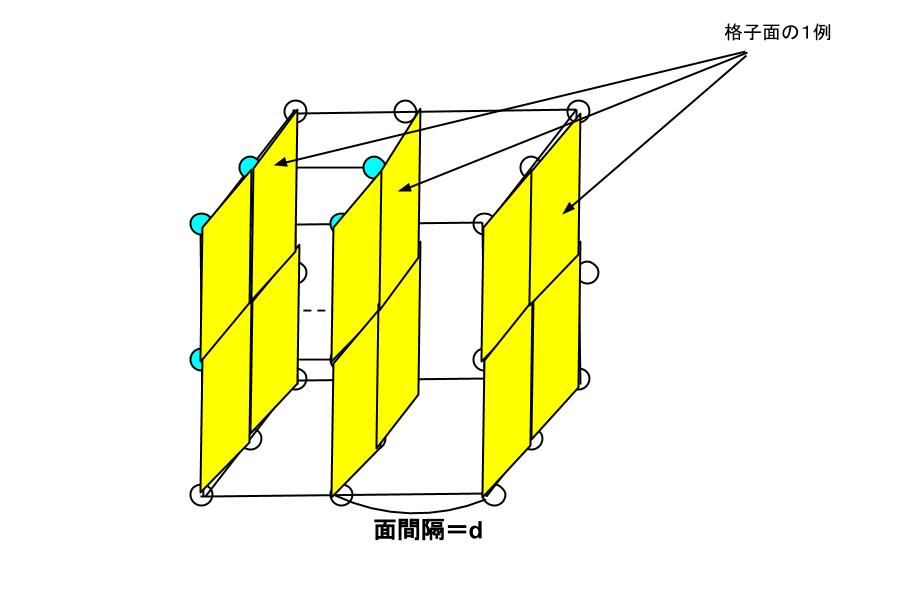
ミラー指数 面間隔d
ミラー指数 面間隔d-ミラー指数が(hkl)の面間隔dhklと,n倍の(nh,nk,nl)である面間隔dnh,nk,nl の関係 n d d hkl ∴ nhnknl = 図・12 {2}面の間隔は, {110}面の間隔の半分である.一 般に,面{nh,nk,nl}の間隔は, {hkl}面の間隔のn分の1である.となります。これは便宜的に格子面間隔が(d/n)の 結晶面(曲n々 n1)面 による一次の回折に対応します。Bragg条 件の一般形とし ては,回 折線はn次 の回折線であっても,い ずれもそれぞれの (hk1)面 からの一次の回折線と便宜上見なし, 図1単 位胞とミラー指数 14
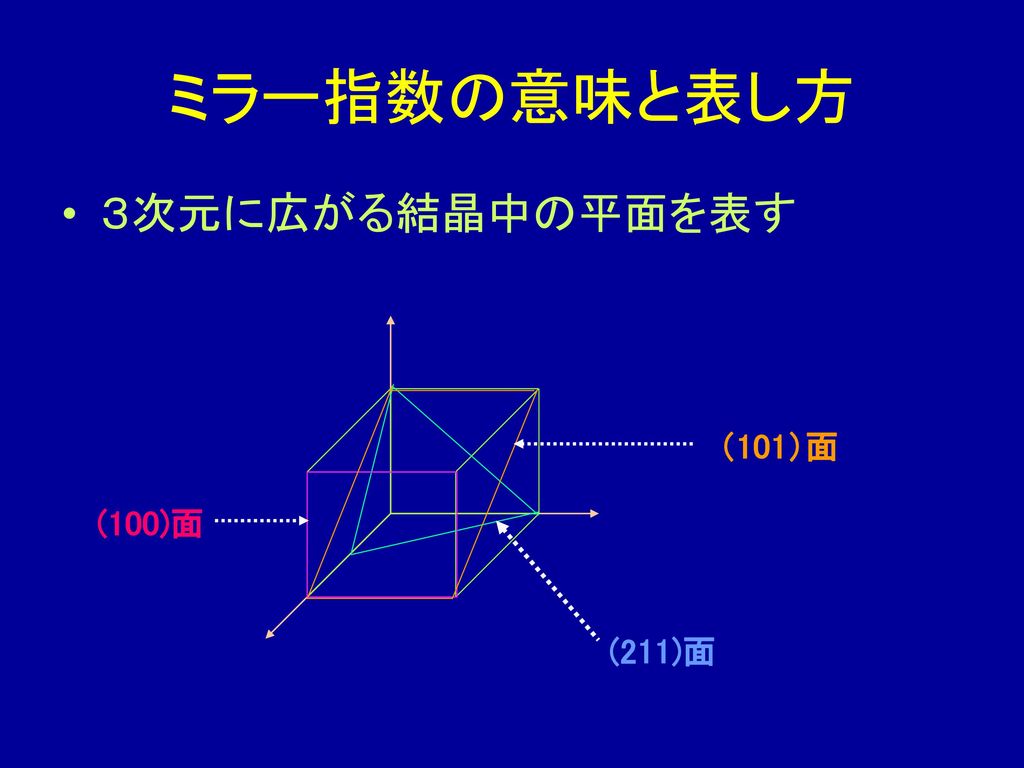



無機化合物の構造と特性 との関係を理解する Ppt Download
(100)面の面間隔をd100 とすると、ja1j = d100 であり、hb1 a1 = q1 a1 = qa1 d100 の関係があ る。また、a1 方向の結晶の長さは、N1 d100 と表される。 従って、sin2 ˇqad100N1 = sin2 ˇqaL はqa = 1=Lのときに0となる。 x 0 05 1 15 2 100 80 40 60 N=10 sin2 (10 px) sin2 (px) h52 x 1/10 9/10 図7 Laue関数 さて、Bragg 条件はq = 2ksin で実際の結晶では互いに平行で等間隔の距離で並んでいる結晶面が無数にならんでいるのです. このような1組の面の集合を結晶格子面といいます. 結晶ではこんな結晶格子面がたくさんあります. これを表したいときに使うのがミラー指数(Miller index)です.ミラー指数 ミラー指数の表記 立方晶における主要な面 立方晶における重要な関係 ( hkl)!hkl dhkl= a h2k2l2 a:格子定数 面間隔 6
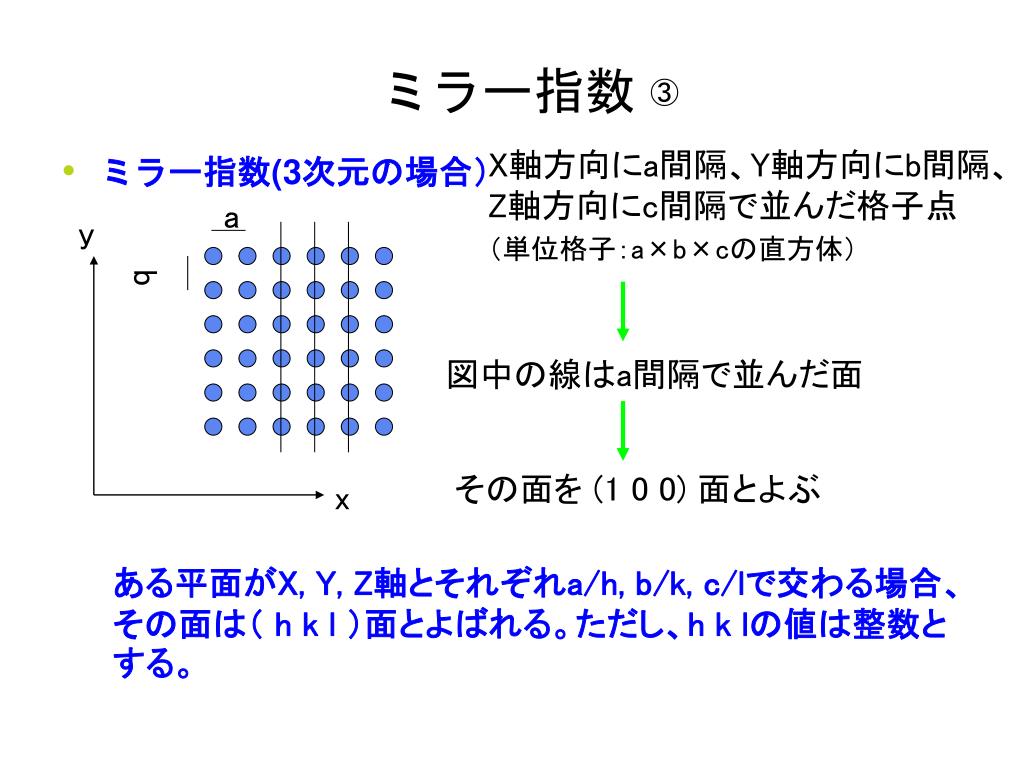
ミラー指数は結晶格子の面や方位を表すために広く使われている表記法で、次のようなルールにしたがって表します。 ミラー指数 表している面または方位 軸を する点を結んで作られる面。 軸の負の方向に する点, 軸を する点を結んで作られる面。 はミラー指数 (h k j l) をもつ格子面の面間隔を求めよ。 六方晶の格子ベクトルは 逆格子ベクトルは c a x y O A a A ミラー指数 (h k j l) をもつ格子面に対応する逆格子は で 面間隔は 応用X軸方向にa間隔、Y軸方向にb間隔で並んだ格子点 (単位格子:a×bの長方形) ミラー指数(2次元の例) a y b 図中の線はa間隔で並んだ直線 その直線を (1 0) と表す x
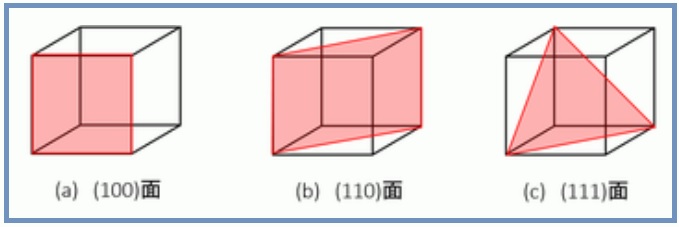
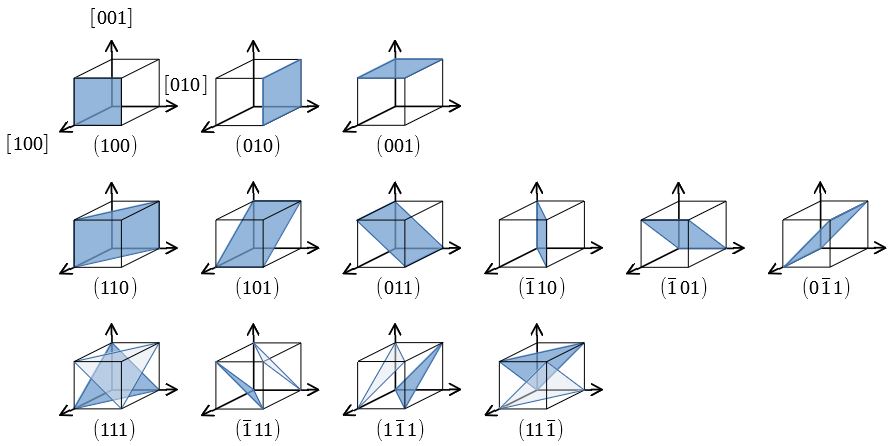
逆格子とミラー指数 8 単位格子のa,b,c軸と(h k l)面を考えると 逆格子ベクトルr* = ha* kb* lc*は(h k l)面と直交し、 (h k l)面の面間隔d (hkl)は1/r*に等しくなる ここで散乱ベクトルkを入射X線ベクトルk 0と 散乱X線ベクトルk 1で表し、その散乱角が2θだとしたらミラー指数(面) 5 仮に,上の単位格子が立方晶だとすると(100),(010),(001) は等価な面です.立方体はa,b,c どの軸で も90 度回せばもとにもどりますから,(100) の図をc 軸の回りに90 度回せば(010) の図になります. (010) の図をa 軸の回りに90 度回せば(001) の図になります.図にはありませんり面とすべり方向の組み合わせを,すべり系(slip system)と呼ぶ. 図23 に,面心立方晶(FaceCentered Cubic),体心立方晶(BodyCentered Cubic)及び六方最密充 填(Hexagonal ClosePacked)の結晶構造を示す.また,表21 にそれらの結晶構造を持った金属材料の




ミラー指数で表された面の図の書き方 化学徒の備忘録



2
原点に最も近い面 原点に近い面と の交点 a 3 原点に近い面と の交点 b b 2 この面を考える 軸との交点 17 2 33 a 軸との交点 b 17 3 22 OB b b 32, 77 hkcc 整数 7 を掛けて h = 3, k = 2 ミラー指数) 面は直接格子の基本並進ベクトル a, a, a を 1 2 3 1/ h, 1/ k, 1/ l で切る平面のことである(ミラー指数のこと)。 (hkl)面とそれに垂直な逆格 子ベクトル K hkl 前ページの図に示すように、 逆格子ベクトル K hkl は(h k l) 面に垂直 であること意味している2つの面での反射が強め合う条件 d Q G Q1 Q2 Q 1 = Q 2 のとき、面での反射波の位相は 常に揃う 622 逆格子空間での逆格子点の方位ベクトル = ミラー指数 (h, k, l) の格子面 = 回析の条件




ミラー指数 Wikipedia



2
構造化学 第6回6月15日 河野淳也 逆格子、Ewald球 1結晶面の指数 hkl方向とは・・・a 1 a 2 a 3 (hkl)面とは・・・a 1方向に1/h, a 2方向に1/k, a 3方向に1/l, で定義される3点を含む平面 h 1 k 1 l 1 r ha 1 ka 2 la 3 ベクトルrの方向 rに意味はない r hkl方向ミラー指数の決め方 とある格子面のミラー指数は、その格子面を無限に延長させたときのx,y,z軸の切片の逆数で表せる。下に具体例を挙げる。 例題 (1,0,0) 上の図の赤く塗られた格子面のミラー指数を考える。 まずx軸の切片は明らかにx=1である。



2



ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら
D実空間格子の(hkl)格子面の間隔 λ光の波長 θ格子面と入射光のなす角 上の式の(hkl)は、格子面のミラー指数である。 ブラッグの反射条件は、結晶によるX線回折を考えるときに使問題1:単純立方格子において、次のミラー指数で与えられる面を図示せよ。 (110) (211) (422) (210) (111) 問題2:半径aの原子がFig 21のように層状に重なっている。面心立方格子(fcc)はABCABC・・・のように重304 ミラー指数 fdenshicom 更新日: 結晶学で等価な原子や原子配列面を参照するために必要な用語のまとめです。
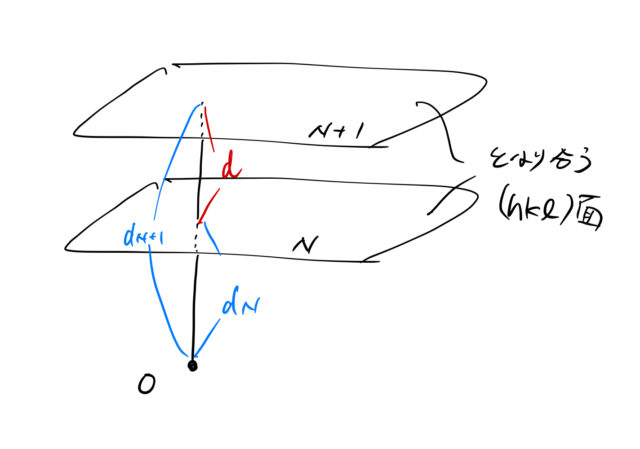



ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら




97 面間隔とミラー指数 Youtube
面間隔 d 光路差}} 入射波 回折波 透過波 結晶面} } 波長 図54 ブラッグ条件の図解。 簡潔明瞭で、極めて実用的。 スカスカな結晶面が、鏡のように反射するしくみが、よくわからない。 結晶面の取り方が無数にあり、結晶面の正体が、はっきりしない。心)や上下面の中心(底心),各面の中心(面 心)のように,元の単位格子の対称性を崩さな いように格子点を加えた格子.全部で14種類 存在する. 体心格子(bodycentered lattice) 底心格子(basecentered lattice) 面心格子(facecentered lattice) 13立方格子の構造を持つ試料として鉄粉を用意し、その内、Si について測定を行い、ミラー 指数、格子定数、面間隔を求めると共に、消滅則の理論用いて結晶構造を決定する。 また、石絵具用原石 ¬種類を測定し、その構成成分について分析を行う。



シリコン格子定数の絶対測定とアボガドロ定数



1
25 格子面群との間の角度であり,sin hkl は連続する結晶格子面間の距離又は面間隔 dhkl と反比例の関係となる. 26 単位格子軸に関連して,格子面の方向と間隔はミラー指数{hkl}により規定される.これらの指数は,結晶面が単位ら(hkl)面 におろした垂線の長さがdで ある。d(hkl) とかくとき,こ れらミラー指数(hkl)を もつ面の面間 隔dと いう意味を表わす。 図2 単位コウシとコウシ定数 図3 ミラー指数 図4・1 トリラウリン粉(1) ミラー指数(h k j l) をもつ格子面の面間隔を求めよ。 (2) 最密六方構造(hcp)における格子定数a とc の関係を求めよ。 4.格子定数a の立方晶のx, y, z 軸をそれぞれa, 25a, 15a および16a, a, 12a で切る 平行な2つの格子面を考える。
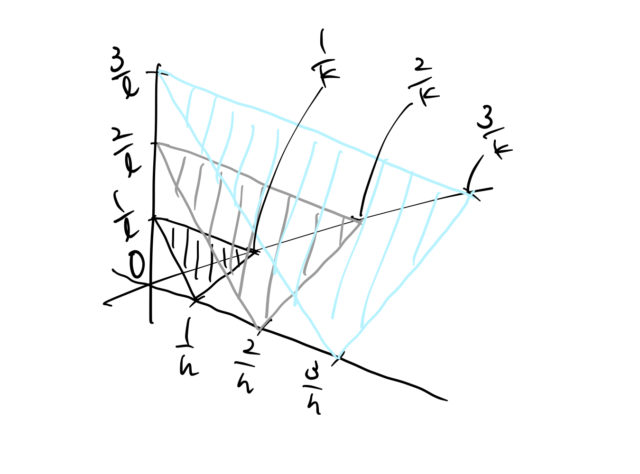



ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら
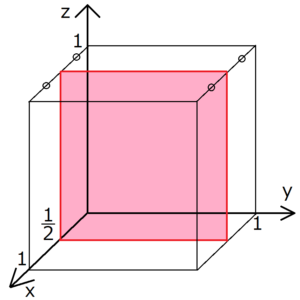



格子面とミラー指数の求め方
4 x線回折 1 目的 銅の粉末試料を用いたx 線回折測定を行い、粉末x 線回折の測定方法と測定原理について学ぶ。 また、得られたx 線回折のデータから格子定数の計算や結晶構造の同定を行えるようになる。 あ わせて、結晶を取り扱う上で重要な逆格子やミラー指数の概念についても理解する。332六方格子のミラー指数 図312六方格子のミラー指数 立方格子との相違→a1,a2,a3,c の4軸を考える点 a1,a2,c 軸をα,β,δで横切る面 a/α :a/β :c/δの最小の整数比h:k:m を求める. 次に最後の指標をl=(hk) のように決める.6 ミラー指数その1:結晶における 方向の記述 7 ミラー指数その2:六方晶における ミラー指数 8 面間隔の求め方 9 格子欠陥(原子空孔と転位)・多結晶体 10 x線の発生法・特性x線について 11 ブラッグの条件と面の間隔 12 粉末x線回折による格子定数の求め方




前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download




電子線照射用試料 B Lial の 育成とその電気的特性の測定 矢萩 橋本研究室 工 E 阿部 信介 Ppt Download
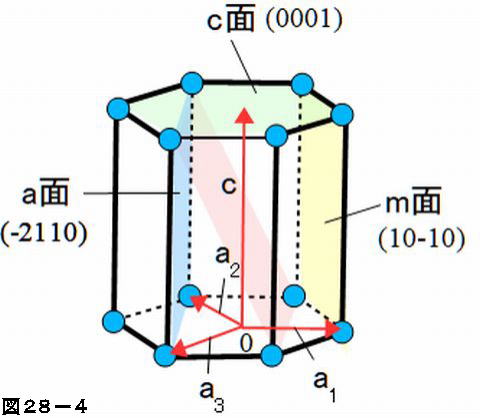
したがって a 面のミラー指数は(2110)であることが分かりますが、ちょうど反対側に当たる(2110)面も等価な a 面です。さらに(1210)、(11)等々いずれも等価な a 面です。このように4つの指数を使うと等価面が指数の組み合わせからすぐにわかります。13 格子面と面間隔 c a b 3a 2b 2c 図3 ミラー指数 単位格子の外形や格子点の並びで構成される格子面あるい は、結晶の原子で構成される原子面を表す方法にミラー指数と 呼ばれるものがある。面の方程式に倣って切片を利用する方法 である。面の方程式は2 (hkl)面と原点との距離(面間隔) ☆面間隔を計算する必要性 ミラー指数(hkl)で表される面どうしの間隔をを計算することは、X線や中性子線回折・ 電子線回折等を用いて結晶構造を解析する際に不可欠な
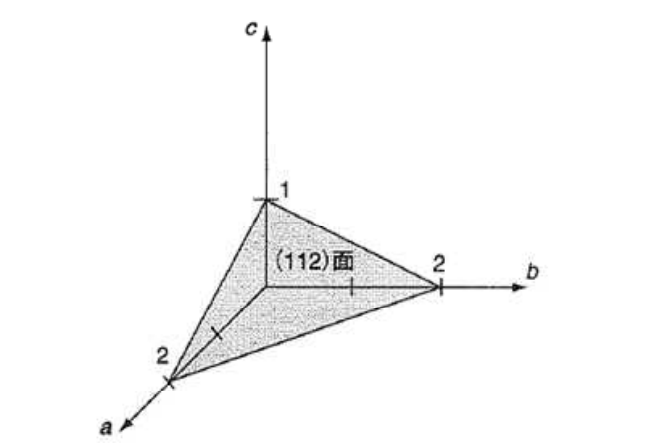



ミラー指数



2
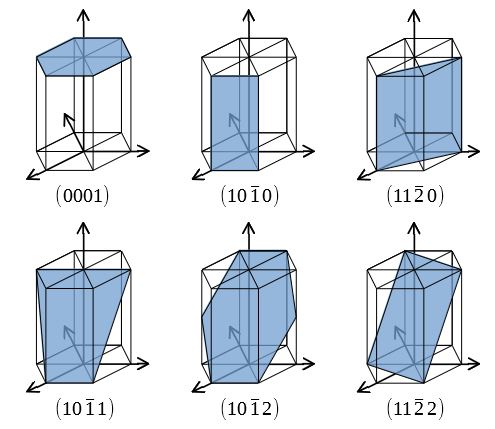
合わせh, k, l を面のミラー指数といい,この面に平行で等間隔な面の集合を (h k l) と表す.ただし六方晶では – (h k) = i とおいて,(h k i l) と表す 図15 いろいろな面のミラー指数 右の面はa, b, c 軸と1a, 2b, 3c で交わる.D:格子面間隔 λ:X線の波長 θ:ブラッグ角 n:整数(n=1,2,3,) で表される。粉末X線回折法では、X線の入射角度と観測角 度が同じになるように走査してX線回折パターンを測定し、 得られた各回折線にブラッグの式を用いることで格子面間結晶面の指数 hkl方向とは・・・ a 1 a 2 a 3 (hkl)面とは・・・ a 1方向に1/h, a 2方向に1/k, a 3方向に1/l, で定義される3点を含む平面 h 1 k 1 l 1 r ha 1 ka 2 la 3 ベクトルrの方向 rに意味はない r hkl方向と(hkl)面は垂直(立方晶の場合)
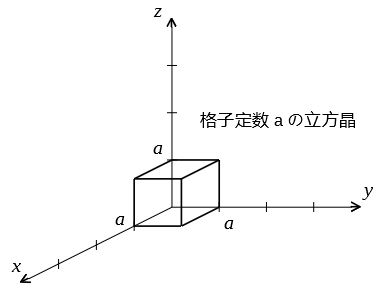



ミラー指数による立方晶 六方晶における面と方向の表し方
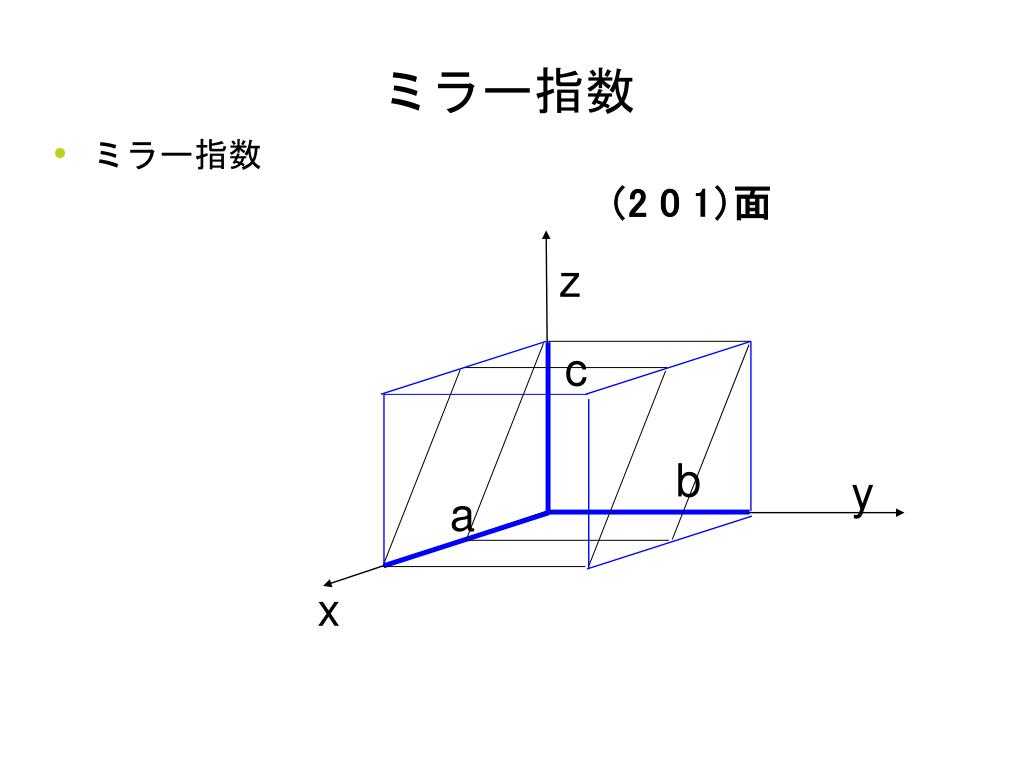



Ppt ミラー指数 2 次元の例 Powerpoint Presentation Free Download Id
ミラー指数の考え方が全然わかりません!解法として結晶面がx,y,z軸とa,b,cで交差するときa,b,cの逆数にa,b,cの最小公倍数をかけた三個の整数<n m l>がミラー指数と説明がありますが、ミラー指数(1 1 1) (1 0 1)など結晶面が軸と交わらないようなものもあり、解き方がわからなくなりま面間隔 指数の隣り合った面間の距離は次の関係で求めることができる。ただし、格子定数を、単位格子の体積をとする。 立方晶: 正方晶: 斜方晶: 六方晶: 単斜晶: 三斜晶: 単位格子の体積 また、単位格子の体積は次の式で求められる。 立方晶: 正方晶: 斜方晶: 六方晶: 単斜晶:ミラー指数が(hkl)の面間隔dhklと,n倍の(nh,nk,nl)である面間隔dnh,nk,nl の関係 n d d hkl ∴ nhnknl = 図・12 {2}面の間隔は, {110}面の間隔の半分である.一 般に,面{nh,nk,nl}の間隔は, {hkl}面の間隔のn分の1である. ミラー指数(hkl)と{hkl},そしてhklの違いは?




Wo14 号 窒化物半導体発光装置 Astamuse



Ppt ミラー指数 2 次元の例 Powerpoint Presentation Free Download Id
ミラー指数の表記 立方晶における主要な面 立方晶における重要な関係 (hkl) !ブラッグの法則についてですが、nλ = 2dsinθの nをミラー指数から求める場合、どのようにすればいいですか? (1,1,0)面、 (6,3,2)面、 (2,3,3)面、 (1,2,3)面など色々な例をあげて解説をお願いします。 例にあげたミラー指数は適当にあげましたが、回折の起き



ミラー指数 面 物理のかぎしっぽ



格子面間隔の計算方法 立方晶 Sciencompass



2



ミラー指数 面 物理のかぎしっぽ




金属の結晶構造 金属材料の基礎知識 オイラーマンの学習帳 備忘録 Evangelist Of Metalworkingfluid



金属材料基礎講座 その23 ミラー指数とは ものづくりドットコム



国家公務員総合職 化学 生物 薬学 H29年 問28解説 薬学 これでok
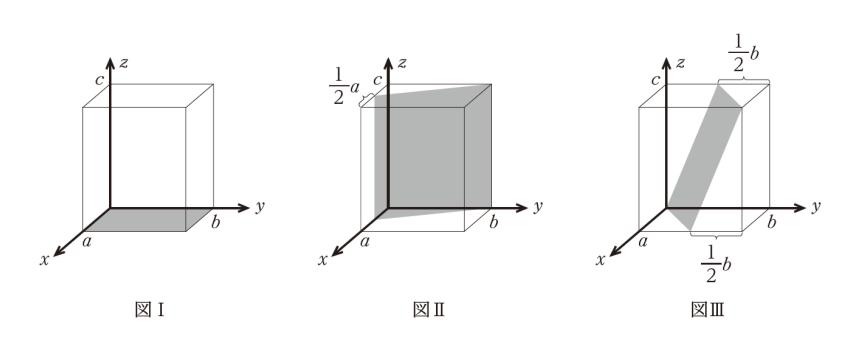



国家公務員総合職 化学 生物 薬学 H29年 問28解説 薬学 これでok




3 ミラー指数についてpart3 Youtube
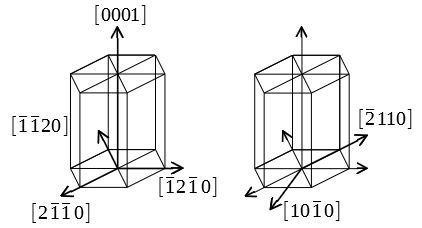



ミラー指数による立方晶 六方晶における面と方向の表し方



2



ミラー指数 面 物理のかぎしっぽ




ミラー指数による立方晶 六方晶における面と方向の表し方
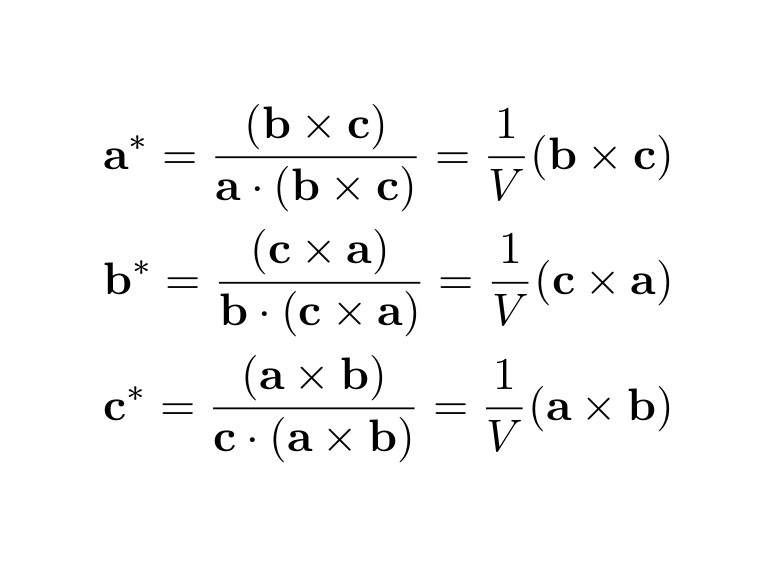



逆格子点の計算の理論背景 Theoretical Background For Calculation Of Reciprocal Lattice And Reciprocal Lattice Points To Cause Diffraction




ミラー指数 方向 2710 ミラー指数 方向 角度 Mbaheblogjpnmry
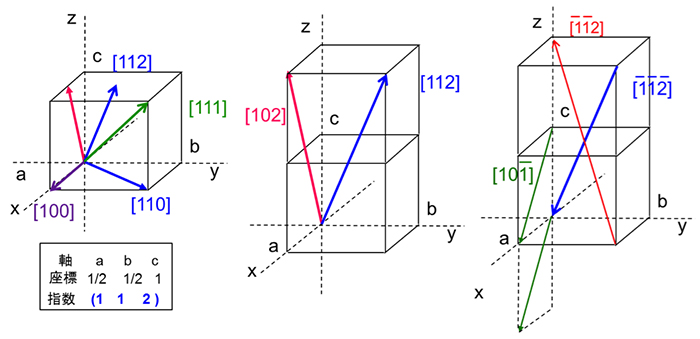



ダイヤモンドの結晶と欠陥 中央宝石研究所 Cgl




ミラー指数 Wikipedia




立方晶の面指数 ミラー指数 についてです 先日 テストに出た問題について Okwave



2



粉末x線回折測定法の原理と利用法 薬学 これでok



放課後化学講義室 X線回折のデータ解析をするプログラム




Xrdの原理と解析方法 わかること x線回折装置とは



のミラー指数 方向指数 の求め方が分かりません 教えて下さい Yahoo 知恵袋




ミラー指数 面指数 ポップラーン
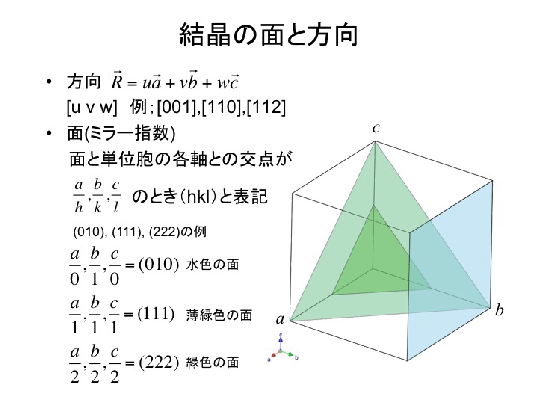



結晶の面と方向の記述方法



ミラー指数 方向 2710 ミラー指数 方向 角度 Mbaheblogjpnmry




無機化合物の構造と特性 との関係を理解する Ppt Download



x線結晶解析におけるラウエの条件式とブラッグの条件式




04 号 x線回折による応力測定法 Astamuse



Information



2
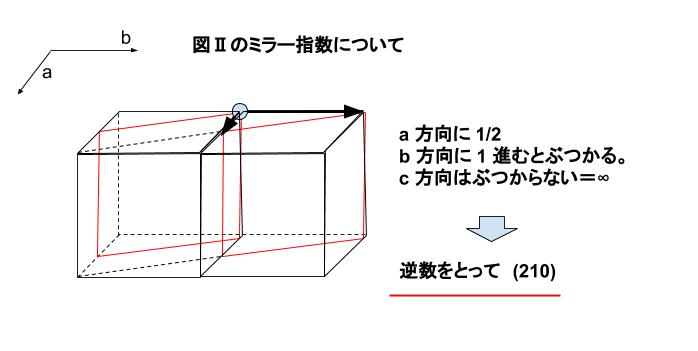



国家公務員総合職 化学 生物 薬学 H29年 問28解説 薬学 これでok



ミラー指数 面 物理のかぎしっぽ
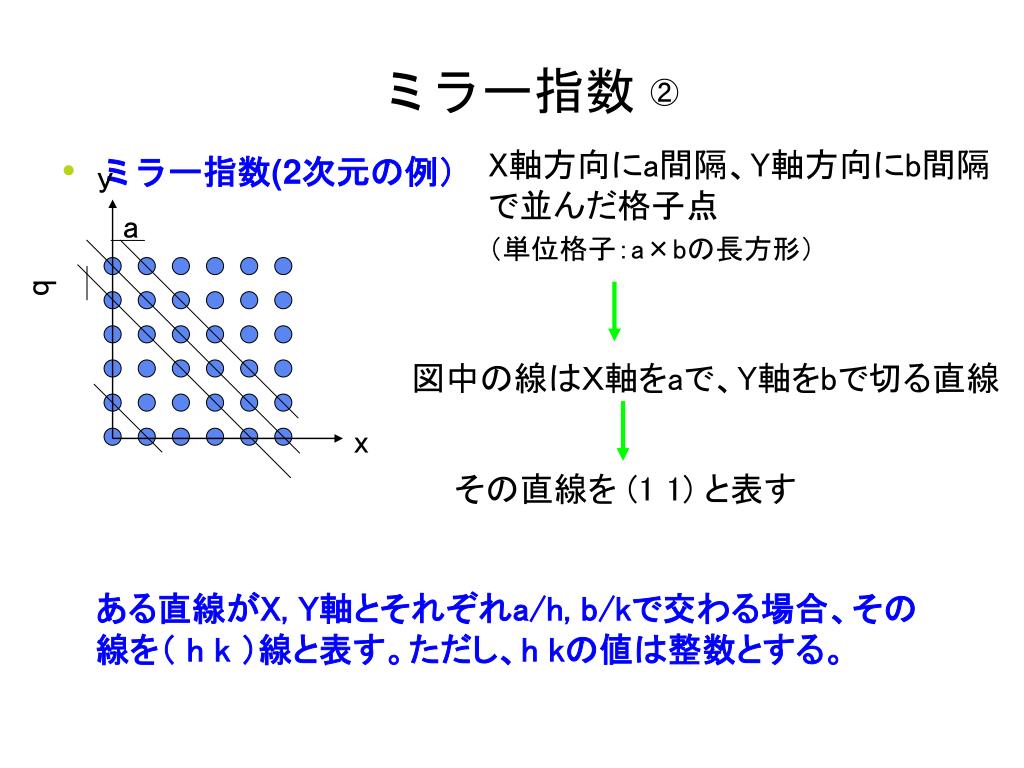



Ppt ミラー指数 2 次元の例 Powerpoint Presentation Free Download Id



ミラー指数による立方晶 六方晶における面と方向の表し方



半導体物理学



2



ミラー指数による立方晶 六方晶における面と方向の表し方




ミラー指数で表された面の図の書き方 化学徒の備忘録



面のミラー指数を求める練習問題が解けず困っています 下の図のhとiのミ Yahoo 知恵袋



格子面とミラー指数の求め方



2



2



1



ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら
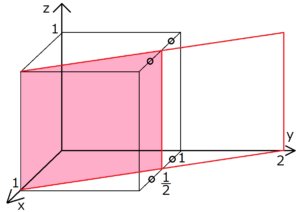



格子面とミラー指数の求め方



面のミラー指数を求める練習問題が解けず困っています 下の図のhとiのミ Yahoo 知恵袋




ミラー指数 面指数 ポップラーン



2
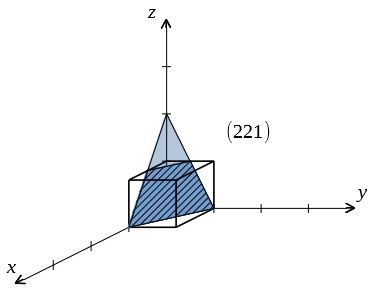



ミラー指数による立方晶 六方晶における面と方向の表し方




ミラー指数 Monozukuri Hitozukuri 日本のものづくり



2




専門 講義 ミラー指数について 大学生 専門学校生 社会人 Clearnote




ミラー指数で表された面の図の書き方 化学徒の備忘録



2
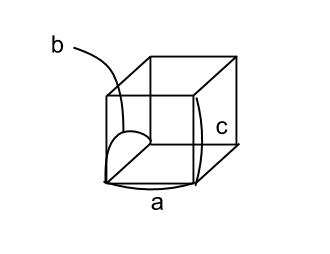



粉末x線回折測定法の原理と利用法 薬学 これでok



5 5
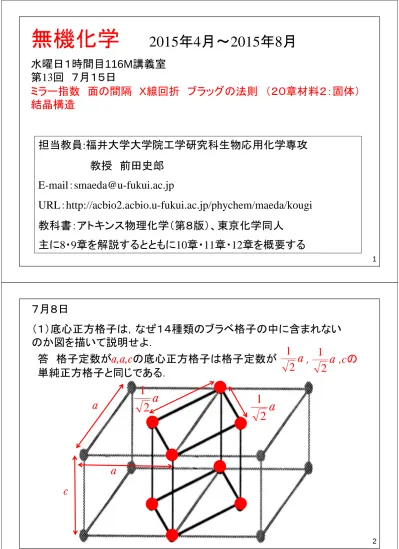



Microsoft Powerpoint 13 15jul15 Ppt



データの解析 鉱物種の同定 戻る まず x線粉末回折で得られた下の回折チャート 特性x線 cuka 1 5418aで測定 を例として説明する 最初は x線回折データは回折チャートのピークの頂点 黒の三角矢印で示したのがピークの頂点 が



2



2
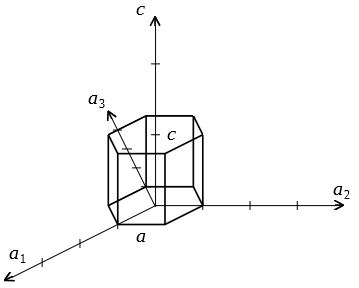



ミラー指数による立方晶 六方晶における面と方向の表し方
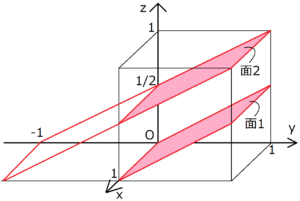



格子面とミラー指数の求め方
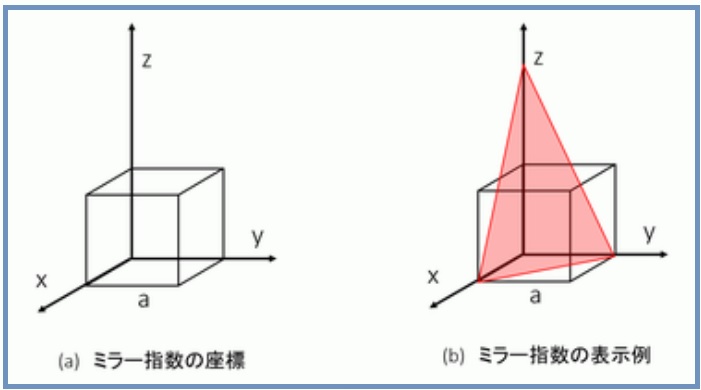



金属材料基礎講座 その23 ミラー指数とは ものづくりドットコム



1



1
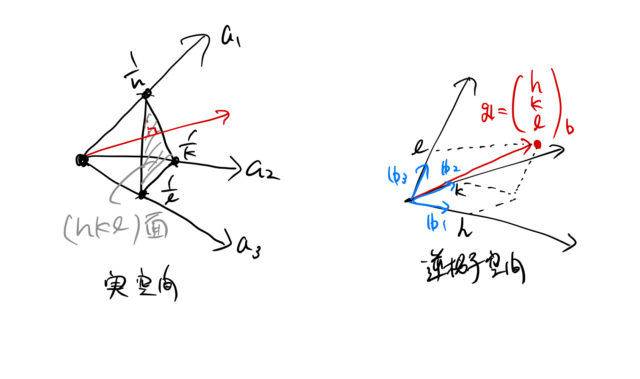



ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら




ミラー指数で表された面の図の書き方 化学徒の備忘録




14 号 圧電振動子 超音波プローブ 圧電振動子製造方法および超音波プローブ製造方法 Astamuse
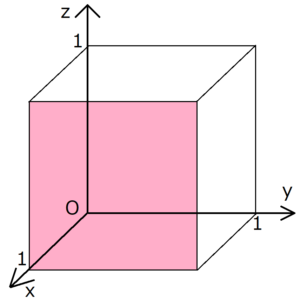



格子面とミラー指数の求め方



ミラー指数が 101 のとき格子面が図のようになりました この Yahoo 知恵袋




1 ミラー指数についてpart1 ゆっくり Youtube




ミラー指数 方向 2710 ミラー指数 方向 角度 Mbaheblogjpnmry
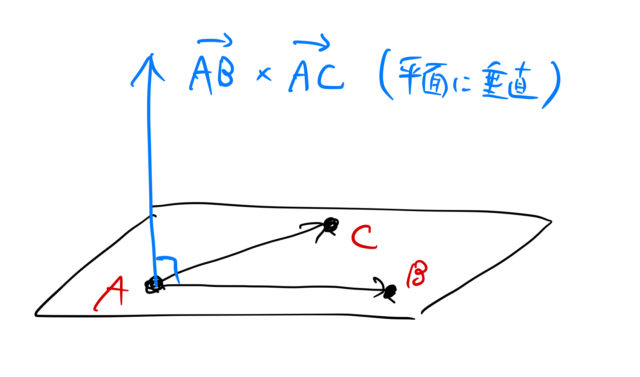



ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら




専門 講義 ミラー指数について 大学生 専門学校生 社会人 Clearnote



2
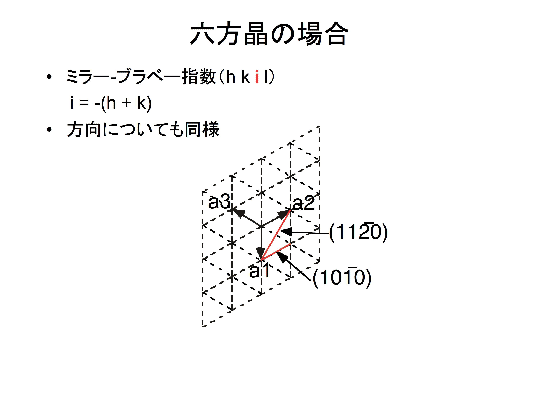



結晶の面と方向の記述方法
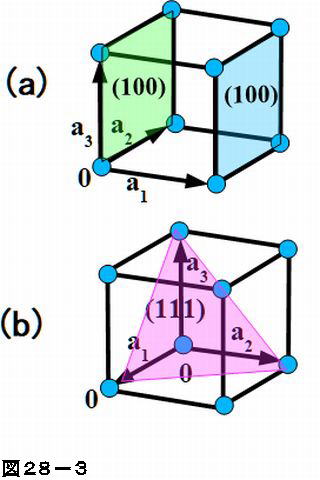



半導体物理学
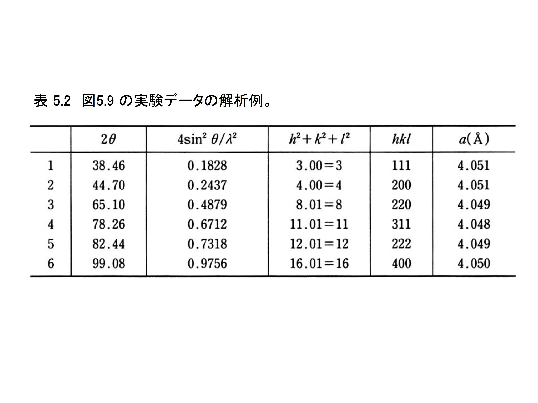



粉末x線回折による解析例



この画像のミラー指数は何かわかりますか またどのように求めたかも教 Yahoo 知恵袋



2



ミラー指数 110 の図を真ん中に書いたのですが 面間隔とは左か右かどち Yahoo 知恵袋



結晶面の面間隔



シリコン格子定数の絶対測定とアボガドロ定数



No comments:
Post a Comment