Let f(x;y) = sin(x2 y2) x2 y2 Then nd lim (x;y)!(0;0) f(x;y) Solution We can compute the limit as follows Let r2 = x2 y2 Then along any path r(t) = hx(t);y(t)isuch that as t !1, r(t) !0, we have that r2 = krk2!0 It follows that lim (x;y)!(0;0) f(x;y) = lim r2!0 sinr2 r2 = lim u!0 sinu u = 1 A Havens Limits and Continuity for, ,c w xyz x t y t z t= = = = sin sin ; Find the limit using the polar coordinates `x=rcos(theta)` , `y=rsin(theta)` , `r=sqrt(x^2y^2)` ` lim_(x,y>0,0) (x^2*y^2)/sqrt(x^2y^2)` We must know that r is approaching 0 from the right when
Content Graphing The Trigonometric Functions
Sin(x^2 y^2)/(x^2 y^2) limit
Sin(x^2 y^2)/(x^2 y^2) limit- Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeDerivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series {\sin\cos} \bold{\ge\div\rightarrow} \bold{\overline{x}\space\mathbb{C}\forall} Tangent of y=x^{2}, at (2,4) en Related Symbolab blog posts Slope




Evaluating Limits Analytically Ppt Download
1 Stewart 5 pts Find the limit or say why it does not exist lim (x;y)!(0;0) x2 sin2 y x2 2y2 Solution The limit is equal to zero To see this, use the Squeeze Theorem Since x 2 x 2y2, we have x2 x22y2 1, therefore 0 2 x2 sin y x2 2y2 sin2 y Since sin2 y goes to zero as x;y go to zero, the middle term does also 2 Stewart 14Log in here We have to find lim (x,y)> (0,0) sin (x^2y^2)/ (x^2y^2) Let x^2 y^2 = t => Substituting t = 0 gives 0/0 which is indeterminate Use l'Hopital's rule and substitute sin t andI Limits in y 0 6 y 6 √ 4 − x2, so the positive side of the disk x2 y2 6 4 I Limits in z 0 6 z 6 p 4 − x2 − y2, so a positive quarter of the ball x2 y2 z2 6 4 2 z x y 2 2 Triple integral in spherical coordinates Example Change to spherical coordinates and compute the integral I = Z 2 −2 Z √ 4−x2 0 Z √ 4−x2−y2 0 y p
Tentukan dw dt (dalam t) 2 Tentukan w t ∂ ∂ 2 2 ;EXAMPLE 1412 We have seen that x2 y2 z2 = 4 represents a sphere of radius 2 We cannot write this in the form f(x,y), since for each x and y in the disk x 2 y 2 < 4 there are two corresponding points on the sphere lim (x^2*sin^2 (x))/ (x^22x^2) = lim x^2sin^2 (x)/3x^2 = sin^2 (x)/3 = 0 (x,x)> (0,0) (x,x)> (0,0) And by letting both x and y = 0, both of which gave me the limit as being equal to 0 (left out equation, but can add in case I'm doing something wrong)
Figure 1321 shows several sets in the xy plane In each set, point P 1 lies on the boundary of the set as all open disks centered there contain both points in, and not in, the set In contrast, point P 2 is an interior point for there is an open disk centered there that lies entirely within the setCos , sina w x y y x x t y t= − = =Find stepbystep Calculus solutions and your answer to the following textbook question Find the limit, if it exists, or show that the limit does not exist limit (x,y) tends to (0,0) y^2sin^2x/x^4y^4



2




Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11
Login Create Account Class11science » Maths lim x tends to y (sin 2 xsin 2 y) / ( x 2 y 2) Share with your friends Share 2 Section 21 Limits In this section we will take a look at limits involving functions of more than one variable In fact, we will concentrate mostly on limits of functions of two variables, but the ideas can be extended out to functions with more than two variables(x2 y2)3=2 = 0 and hence lim (x;y)!(0;0) x4 y4 (x2 y2)3=2 = 0 6 Find the limit if it exists, or show that the limit does not exist lim (x;y;z)!(0;0;0) xyz x2 y2 z2 Hint Consider using spherical coordinates x = ˆsin˚cos , y = ˆsin˚sin , z = ˆcos˚ Solution Using spherical coordinates x = ˆsin˚cos , y = ˆsin˚sin , z = ˆcos



Solved Please Show Your Work Step By Step In Order To Get Chegg Com




Practice Problems For Exam 2 With Solution Calculus I Math 1210 Docsity
2 −π3 −π π −π2 3π 2π y x ตัวอย 1าง พิจารณาลิมิตทางซ ายของ fx()sinx x = ที่ 0 จะได ว า f ()x มีค าเข าใกล ค าคงตัว 1 เมื่อ x →0− นั่ือ นค 0 sin lim 1 x x → − x พิจารณาลิมิตทางขวาของ fx()sinx2 0 Z x x2 y2xdydx Solution integral = Z 2 0 Z x x2 y2xdydx = Z 2 0 " y3x 3 # y=x y=x2 dx = Z 2 0 x4 3 − x7 3!X0 = cos(y) y0 = sin(x) See if you can sketch the direction eld ( nd/classify the equilibria rst!) SOLUTION See the homework solutions to Chapter 9 4 14 A spring is stretched 01 m by a force of 3 N A mass of 2 kg is hung from the spring and is also attached



Mapleprimes Com




The Tangent To The Curve Y E 2x At The Point 0 1 Meets X Axis At
Respuestas a la pregunta Límite lim (x, y) → (0,0) sin (x2 − y2) x2 − y2lim (x, y) → (0,0) sin (x2 − y2) x2 − y2 \ lim \ limits _ {(x, y) \ to (0,0See the answerSee the answerSee the answerdone loading Evaluate the limit using the substitution z=x^2y^2 and observing that z>0 if and only if (x,y)>(0,0) lim(x,y)>(0,0) 12 By considering di erent paths of approach show that the function f(x;y) = x4=(x4 y2) has no limit as (x;y) approaches (0;0) Solution The limit as y = 0 and x !0 is equal to 1 The limit as x = 0 and y !0 is 0 Therefore, the limit of f(x;y) as




117




Calculate The Next Limit If It Doesn T Exist Then Prove It 2 Y B Lim X Y 0 0 Homeworklib
Sin , sinx y b w e x s t y t s = = = 2 2 ln ;Let the point (x, y) → (0, 2) along the line y = 2 in the coordinate plane, then the given limit becomes = lim(x →0){ sin(2x)/x } = 2 lim(x→0) {sin(2x)/2x} = 2 lim x tends to y (sin2xsin2 y) / ( x2 y2) Maths Limits and Derivatives NCERT Solutions;




The Squeeze Theorem




Use Polar Coordinates To Find The Limit Hint Let X R Co Quizlet
I want to prove the following limit \lim_{x\rightarrow 0} \frac{\sin x}{x^{2}}=\infty using the definition of limitBecause the rst factor, (x y), goes to 0, and everything else is bounded This proves the di erentiability at the origin On the other hand, the partial derivatives are not continuous Ideed, for x6= ywe have f x(x;y) = 2(x y)sin 1 x y cos 1 x y and f y(x;y) = 2(x y)sin 1 x y cos 1 x y For both partial derivatives, ifThe function, z = f(x,y), increases most rapidly at (a,b) in the direction of the gradient (with rate ) and decreases most rapidly in the opposite direction (with rate ) EX 2 For z = f(x,y) = x2 y2, interpret gradient vector ∇f(a,b) ^ ^ ∇f(a,b) ⇀ ⇀



Limit Of Sin X 2 Y 2 X 2 Y 2 Using Polar Coordinates And L Hopital S Rule Youtube



Use Polar Coordinates To Find X Y 0 0 Lim Sin X 2 Y 2 X 2 Y 2 You Can Also Find The Limit Using L Hopital S Rule Bartleby
EXAMPLE 2 Evaluate limit lim θ→π/2 cos2(θ) 1−sin(θ) Since at θ = π/2 the denominator of cos2(θ)/(1− sin(θ)) turns to zero, we can not substitute π/2 for θ immediately Instead, we rewrite the expression using sin2(θ)cos2(θ) = 1 lim θ→π/2 1−sin2(θ) 1−sin(θ) = lim θ→π/2 (1−sin(θ))(1sin(θ)) (1−sin(θ))$$\lim_{x \to 0^}\left(\frac{\sin{\left(2 x \right)} \tan{\left(x \right)}}{x^{2}}\right) = 2$$ Más detalles con x→0 a la izquierda $$\lim_{x \to 0^}\left(\fracSolved example of limits lim x → 0 ( 1 − cos ( x) x 2) \lim_ {x\to0}\left (\frac {1\cos\left (x\right)} {x^2}\right) x→0lim ( x21−cos(x) ) Intermediate steps Plug in the value 0 0 0 into the limit




Answered 36 6x2 Y2 2 Evaluate The Limit Using Bartleby




Gaussian Integral Wikipedia
Solve the Nonlinear System of Equations x^2 y^2 Finding the Coterminal Angle of Least Positive Mea Limit of sin(x^2 y^2)/(x^2 y^2) using Polar Co Multivariable Calculus The Limit of x/(x y) as ( Parametric and Symmetric Equations given a Point a Equation of Conic with Eccentricity = 2/3 Focus (0 Solve 2sin^2(x) 3sinGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



Is X2 Y2 Sin 1 X2 Y2 Differentiable Quora




Lim X Y Sin 2x Sin 2y X 2 Y 2 B Lim Sin X Sin 39 Yx
Now lim sin 2 y = 0 y → 0 So by the squeeze theorem 0 ≤ ( x 2 sin 2 y) / ( x 2 2y 2) ≤ 0 And therefore lim ( x 2 sin 2 y) / ( x 2 2y 2) = 0 ( result ) (x,y) → (0,0)Use the squeeze theorem evaluate lim(x,y)→(0,0) sin(x^2y^2)/x^2y^2 To apply the Squeeze Thoerem we must select functions g and h Use the Taylor Polynomials of degree 1 and 3 as natural bounds of sinusinu to fill in the blanks _____≤ sin(x2y2) ≤_____ Dividing by x^2y^2 we get _____≤sin(x^2y^2)/x^2y^2 ≤_____Try writing it as $$\frac{\sin(xy^2)}{x^2y^2}=\frac{\sin(xy^2)}{xy^2}\frac{xy^2}{x^2y^2}$$ Then $$\frac{\sin(xy^2)}{xy^2} \rightarrow 1$$ So you just have to evaluate the limit of $$\frac{xy^2}{x^2y^2}$$ which is zero since $$\frac{xy^2}{x^2y^2}=\frac{x}{(\frac{x}{y})^2 1} \leq



Graphs Root




Limit Of 1 Cos X X As X Approaches 0 Video Khan Academy
X 2sin y x 22y ≤ sin2 y The limits of the outer two functions as (x,y) → (0,0) are both 0, and so the Squeeze Theorem tells us that lim (x,y)→(0,0) x2 sin2 y x2 2y2 = 0 The notion of the limit of a function of two variables readily extends to functions of three or more variables Explanation sin2A− sin2B = sin(A− B) ⋅ sin(A B) L = lim y→x sin2y − sin2x y2 −x2, We know that , y → x ⇒ (y − x) → 0 ∴ L = lim (y−x)→0 sin(y − x)sin(y x) (y − x)(y x) ∴ L = lim (y−x)−0 sin(y −x) y − x ⋅ lim y→x sin(y x) y x ∴ L = (1) ⋅ sin(x x) x x,as, lim θ→0 sinθ θ = 1,θ = (y − x) ∴ L = sin2x 2x Answer link574 Evaluate a triple integral using a change of variables Recall from Substitution Rule the method of integration by substitution When evaluating an integral such as ∫3 2x(x2 − 4)5dx, we substitute u = g(x) = x2 − 4 Then du = 2xdx or xdx = 1 2du and the limits change to u = g(2) = 22 − 4 = 0 and u = g(3) = 9 − 4 = 5



Evaluate Lim X Y 0 0 Cos X 3 Y 2 X Y 2 If The Limit Exists Sarthaks Econnect Largest Online Education Community




Limits By Factoring Video Khan Academy
3 , 2x y b w e y e x x t y t= − = = 2 2 ;X2 y2 sin 1 x y = 0;Limit as (x,y) approaching (0,0) of (xy)/ (x^2y^2) \square!




Limit Of X 3 Sin Y X 6 2y 3 As X Y To 0 0 Mathematics Stack Exchange



2
So let's consider some assumptions for this problem It is given that (x,y) approaches to (0,0) So both will be equivalent only let's consider { x= y= x} Here x and y values will be euivalent to each other Now we have { (Lt x tends to 0 ) ( Lt y tends to 0) sin x^2 /Xy 2 sin x y 2 The Law of Sines sinA a = sinB b = sinC c Suppose you are given two sides, a;band the angle Aopposite the side A The height of the triangle is h= bsinA Then 1If a Keeping this in mind, we can factor an x from the denominator of the fraction, giving =lim_(xrarr0)(sinx)/(x(2x1) We can rearrange this to get sinx/x, which we already know the limit of =lim_(xrarr0)(sinx/x)1/(2x1) Limits can be multiplied, as follows =lim_(xrarr0)sinx/x*lim_(xrarr0)1/(2x1) Since lim_(xrarr0)sinx/x=1, the expression simply equals




The Slope Of The Normal To The Curve Y 2x 2 3sin X At X 0is A 3 B 1 3 C 3 D 1 3



Content Graphing The Trigonometric Functions
Lim (x,y)>(0,0) xy^4 / (x^2 y^8) Natural Language;2Consider f(x) = sin(2x 7)cos(x2) cos2(4 x3) x Find lim x!1f(x), if this limit exists (Solution)This limit may look daunting, but we need only recall that the sine and cosine functions are bounded Since sine and cosine take values between 1 and 1, the values of the product sin(2x 7)cos(x2) will be between 1 and 1 That is,Dx = " x5 15 − x8 24 # 2 0 = 32 15 − 256 24 = − 128 15 07 Example Evaluate Z π π/2 Z x2 0 1 x cos y x dydx Solution Recall from elementary calculus the integral R cosmydy = 1 m sinmy for m independent of y Using this




Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11



Kth Instructure Com
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music θ y = r sin θ r 2 = x 2 y 2 We are now ready to write down a formula for the double integral in terms of polar coordinates ∬ D f (x,y) dA= ∫ β α ∫ h2(θ) h1(θ) f (rcosθ,rsinθ) rdrdθ ∬ D f ( x, y) d A = ∫ α β ∫ h 1 ( θ) h 2 ( θ) f ( r cos Calculus Find dy/dx sin (xy)=x^2y sin(xy) = x2 − y sin ( x y) = x 2 y Differentiate both sides of the equation d dx (sin(xy)) = d dx (x2 − y) d d x ( sin ( x y)) = d d x ( x 2 y) Differentiate the left side of the equation Tap for more steps Differentiate using the chain rule, which states that d d x f ( g ( x)) d d x f




L Hopital S Rule Limit At 0 Example Video Khan Academy




How To Compute The Lim X Y To 0 0 Frac X 2 X 2 Y 2 Mathematics Stack Exchange
, s a w x y x x y s t t = − = = 2 3 2 sin( ) ;Take the limit of each term Tap for more steps Split the limit using the Limits Quotient Rule on the limit as x x approaches 0 0 ( lim x → 0 2 x cos ( x 2)) ( lim x → 0 1) ( lim x → 0 2 x cos ( x 2)) ( lim x → 0 1) Move the term 2 2 outside of the limit because it is constant with respect to x xAnswer to Find the limit or show that the limit does not exist \\lim_{(x,y)\\rightarrow (0,0)} \\sin (\\frac{\\pi x^2y^2}{x^4y^4}) By signing up,




Finding Rational Parametric Curves Of Relative Degree One Or Two Pdf Free Download




14 1 Functions Of Several Variables Mathematics Libretexts




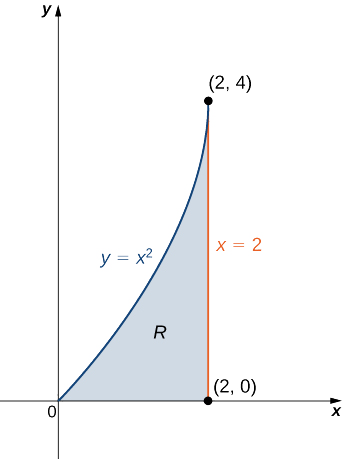
The Area Bounded By Y Sin X And 2x Pi Y Is



Trigonometric Identities




Samacheer Kalvi 11th Maths Solutions Chapter 9 Limits And Continuity Ex 9 6 Samacheer Kalvi




Evaluating Limits Analytically Ppt Download




Calc 501 1000 By James Bardo Issuu




Notes On Maple Computer Assignment You Can Do Your Maple Assignment In Math Department On The 5th Floor Pdf Free Download



Solved Find Limit Of A X Y Function Lim X Y Tends To Chegg Com




Fall Exam 16 Questions And Answers Math 1004 Calculus For Studocu




14 2 Limits And Continuity




Pdf Family Of Circles Tarun Gehlot Academia Edu
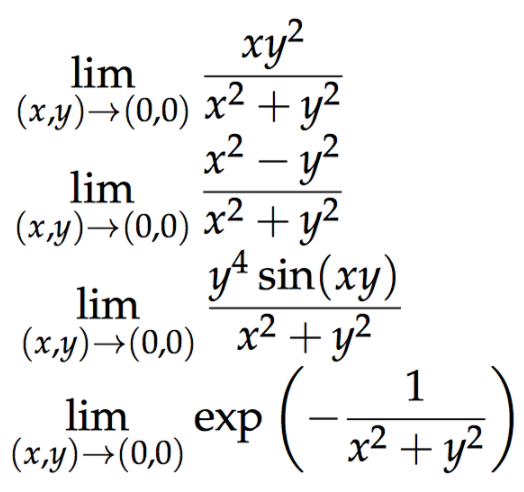



Evaluate The Limits Or Explain Why It Does Not Exist 2 Im X Y 0 0 X 2 Y2 2 2 Lim X Y 0 0 X2 Y2 X Y 0 0 X2 92 X Y 0 0 P Lim




Underset X Rarry Lim Sin X Sin Y X Y



3




Limit Of Sin X 2 Y 2 X 2 Y 2 Using Polar Coordinates And L Hopital S Rule Math Videos Sins Calculus




Sheet 3fk Pdf




Consider The Function F X Y Sin Pi X2 Y2 X2 Y2 A What Are The Domain And Range Of This Function B Does A Limit Of F X Y Exist At The Origin If So



Wwwf Imperial Ac Uk



Evaluate The Following Limit Lim X 0 2 Cos X Sin X P 4 X 2 Sarthaks Econnect Largest Online Education Community



Quickref Calc Pdf




X Y A 0 M 1 X A Y1y1 M 2 X A Y2y2 Y2y2 Y1y1 M 1 X A M 2 X A M1m1 M2m2 Y 0 M X A Point Slope Ppt Download




Solved 1 Point Find The Limit Of The Function Sin 2 X Chegg Com



2 4 Continuity Calculus Volume 1



2




Example 17 Prove Sin 5x 2 Sin 3x Sin X Cos 5x Cos X



Solved Evaluate The Following Limits Or Use The 2 Path Test To Show That The Limit Does Not Exist A Lirn Sin Y Sin X X Jij Pll X2 4 B Course Hero



2




1 Soal Dan Pembahasan Limit Fungsi Trigonometri




The Value Of Lim X Gty Sin 2x Sin 2y X 2 Y 2 Equals Youtube



15 6 Calculating Centers Of Mass And Moments Of Inertia Mathematics Libretexts



Evaluate Lim X To 0 Frac X 2 X Sin Frac 1 X Mathematics Stack Exchange



2



Solved Find The Limit If It Exists Or Show That The Limit Does Not Exist Displaystyle Lim X Y To 0 0 Dfrac Y 2 Sin 2 X X 4 Y 4




Y Xy 3 1 X 2 1 2 Y 0 1 Harushley



L Hopital S Rule



Sage Calculus Tutorial Limits At Infinity



微積分統一教學網 考題分析




Calculus Physic Chemistry Accounting Help Tam Cao Nghenhachay Net




Showing A Limit Does Not Exist Youtube




Derivative Calculator Wolfram Alpha




Let F X Y Xy X 2 Y 2 Find Limit Of F X Y As X Y Rarr 0 0 I Along Y Axi Plainmath




Evaluate The Following Limit Limit As X Y Approaches 0 0 Of X 3 Y 3 X 2 Xy Y 2 Study Com




1 Soal Dan Pembahasan Limit Fungsi Trigonometri




1 Consider Lim Z Y 0 0 2 Y2 Compute The Limit Along The Two Lines Y Homeworklib




Limitatinfinity Html




1 The Lower And The Upper Limit Of Z Sin Xy Cos X Cos Y 2 At 0 Download Scientific Diagram



Plot Expression Or Function Matlab Fplot
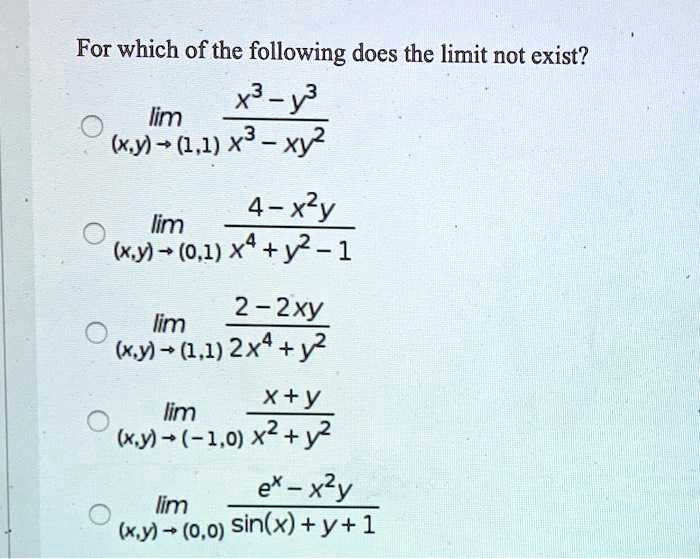



Solved For Which Of The Following Does The Limit Not Exist X Y3 Lim Xy 1 1 3 Xy2 4 Xy Lim Xy 0 1 X4 Y2 1 2 2xy Lim Xy 1 1 2x Y2 Xty




Solved A Find The Limit Lim X Y Gt 0 0 Chegg Com




Triple Integrals Volume And Average Value



2



Sage Calculus Tutorial Limits At Infinity




Rd Sharma Solutions For Class 12 Maths Updated For 21 22 Chapter 11 Differentiation



2




Solution For Quiz 4 Questions Multivariable Calculus Mth 234 Docsity



Answered Find X Y 4 V2r Y 2 18 Lim X Bartleby




The Results For F X Y Sin 4 X2 Y2 Documentclass 12pt Minimal Download Scientific Diagram



Limits And Continuity 11 2




Homework Solution 6 Homework 6 Model Solution Section 14 2 14 3 14 2 6 Find The Limit If It Studocu



3 8 Implicit Differentiation Calculus Volume 1




Solved Evaluate The Two Dimensional Limit Limit X Y Chegg Com




Oneclass Use Polar Coordinates And The Squeeze Theorem To Find Lim X Y Rightarrow 0 0 X3 Y3 X2 Y2 S



2




Weierstrass Substitution Wikipedia



2



Faculty Bucks Edu



3 8 Implicit Differentiation Calculus Volume 1




Lim X Y 0 0 X 2 Sin 2 Y X 2 2y 2 Physics Forums




Wolfram Alpha Examples Step By Step Solutions




Proffesionalintegrationidifferentialcalculus Pdf Curvature Area



2




Let F X Y Xy X 2 Y 2 Find Limit Of F X Y As X Y Rarr 0 0 I Along Y Axi Plainmath



2



3d Surface Plotter Academo Org Free Interactive Education



No comments:
Post a Comment